Faster distance computation for n-th tensor
Table of Contents
Quick summary
- The page represents a faster computation technique of distance matrix when your data is > 3rd tensor.
- Faster approach is 310x faster than a normal approach.
- Sample codes (for Numpy, Pytorch) are available.
Distance matrix? Why we need it?
Machine learning techniques, especially the one using Kernel functions, require the distance matrix. A traditional example is SVM (Support Vector Machine), a recent trend is GP(Gaussian Process). Of course, Deep neural networks use kernel functions.
We need the distance computation for the Kernel function. Many kernel functions, including Gaussian Kernel, are defined with the distance function. Let’s see Gaussian kernel.
where sigma^2 is a bandwidth term, || x -y ||² is a distance function.
When x, y are scaler values, || x – y ||^2 is a piece of cake. However, when x and y are matrix form or a set of n-th tensors? How do we compute || x – y ||^2?
Naive computation: double loop
A naive approach is to use a double loop. Let’s define X and Y firstly. Here X and Y are sets of m data.
The expected distance matrix (D) represents distances between data x and y. So, the distance matrix D has m rows and m columns.
When we write the computation with the double loop, it’s like this way (in Python)
|
1 2 3 4 5 6 |
import numpy as np D = np.zeros((m, m)) for i, x in enumerate(X): for j, y in enumerate(Y): d = (x - y) ** 2 D[i, j] = d |
Even though x and y are more than 2-nd tensor (or array), we can compute D with the double loop.
Bottleneck: Speed
The biggest and critical bottleneck is speed. Python for-loop is slow comparing other languages. If it’s x and y are vectors (X and Y are matrices), we can compute it in an efficient way like the code below.
|
1 2 3 4 |
XY = np.dot(X, Y.T) X_sqnorms = np.diagonal(XX) Y_sqnorms = np.diagonal(YY) D_XY = -2 * XY + X_sqnorms[:, np.newaxis] + Y_sqnorms[np.newaxis, :] |
However, how about x and y in the 2-nd tensor? Let’s say we have X: (100, 32, 12), Y: (100, 32, 12) which means 100 samples of (32 * 12) matrices. If I describe in math. way,
We can NOT use the same code as above because np.dot(X, Y.T) is impossible for our X and Y.
What should we do? A clever guy on StackOverflow gave the elegant answer. The Illustration below shows his elegant idea. We’d like to use pdict() the function cause it’s fast. But pdict() takes only a vector. So, we reshape our matrices to vectors.
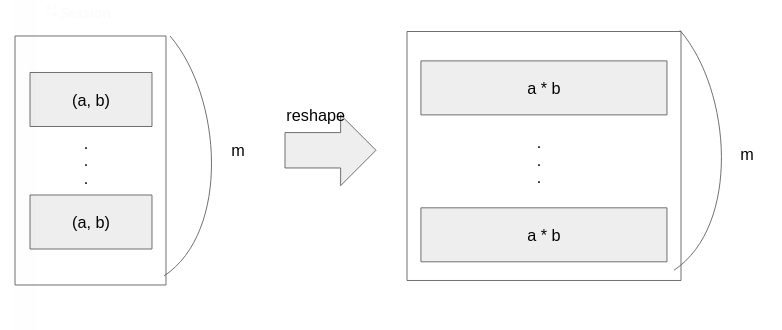
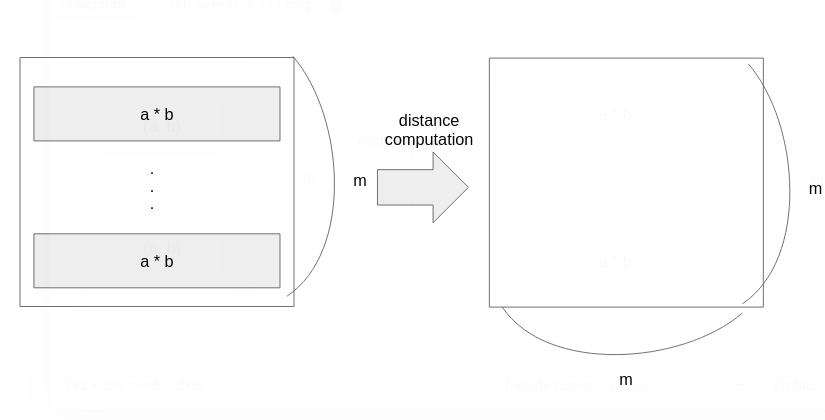
Performance
I implemented comparisons: double-loop v.s. reshape-approach. My tiny code tests the following cases,
- with numpy, D(X, X) where X is (50, 64, 12).
- with pytorch, D(X, X) where X is (50, 64, 12).
- with pytorch, D(X, Y) where X, Y are (50, 64, 12).
The code is available on Gist. I checked results do not have significant value differences between the 2 approaches.
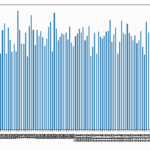
The speed comparisons are here. You see? The reshape approach is 350x time faster than the double for-loop approach.
|
1 2 3 4 5 6 7 8 9 10 11 |
# With numpy D(X, X) euclidean_normal(x_array): 0.0548619776032865 euclidean_n_th_tensor(): 0.0010964786633849144 # With torch D(X, X) euclidean_normal_torch(x_array): 0.215167117677629 euclidean_n_th_tensor_torch(): 0.0006791732273995876 # With torch D(X, Y) euclidean_normal_torch_xy(x_torch, y_torch): 0.2175855808891356 euclidean_n_th_tensor_torch_xy(): 0.022157766856253147 |
I’m a little bit surprised that Pytorch is slower than Numpy at the double for-loop, even though Pytorch’s reshape approach is faster than Numpy.


Discussion
New Comments
No comments yet. Be the first one!